2020. 4. 2. 23:20ㆍArtificial Intelligence
Overview
머신러닝 혹은 딥러닝으로 모델을 학습시키다 보면, 엄청난 양의 행렬 연산이 요구되는 경우가 다반사입니다. 컴퓨터는 이미지, 데이터 분포등의 정보를 벡터들로 구성하여 인식하는 경우가 많기 때문에 대부분의 전처리된 Input Data는 벡터의 모습을 띄게 됩니다.
하지만 때때로 이 전처리된 벡터의 크기는 굉장히 커서, 딥 러닝 모델에 과도한 부하를 주고 학습의 효율을 떨어뜨립니다. 벡터를 구성하는 모든 차원(크기가 n인 벡터라고 할 때 n차원)의 정보가 의미있는 것은 아니며, 의미있는 부분들만 추려내어 차원을 축소시킬 수 있다면, 이는 데이터의 형태(분포)를 유지하면서 데이터의 크기를 줄여 학습의 효율을 높일 수 있을 것입니다.
예를 들어 아래 그림에서 데이터는 3차원 분포를 나타내지만, 실제로 의미있는 분포를 보여주는 데에는 2차원 이어도 충분하다는 것을 짐작할 수 있습니다. 이에 대한 해결책을 제안한 것이 바로 주성분분석(Principal Component Analysis, 이하 PCA)입니다.

Definition
PCA는 분포된 데이터들의 분산을 최대한 보존하면서, 서로 직교하는 기저축들을 찾아 높은 차원의 데이터들을 서로 연관성이 없는 낮은 차원의 데이터들로 변환하는 기법입니다. PCA의 목적은 분산을 최대한 보존하는 기저축들을 찾는데에 있습니다.
이 기저축들을 "주성분"이라 부릅니다. 주성분은 데이터들의 분산이 가장 큰 방향벡터를 의미합니다. 즉, 방향벡터가 가리키는 방향을 따라 데이터들의 분산(흩어진 정도)가 가장 크다는 것을 의미합니다. 분산을 잘 보존하고 있다는 것은, 실제 데이터들의 분포를 잘 반영하고 있다는 것으로 해석할 수 있으므로 차원축소가 효과적으로 이루어졌다는 것을 의미합니다.
X를 n개의 차원을 가진 벡터라 하고, Z를 축소할 p의 차원을 가진 벡터라고 한다면, 다음과 같은 과정을 거쳐 X의 모든 벡터들이 서로 직교하는 p차원의 벡터들로 선형변환 될 수 있을 것입니다. PCA의 목표는 X의 분산을 최대한 보존하면서 Z를 만들어내는 선형변환 A를 찾아내는 것입니다.

Covariance Matrix
결론부터 말씀드리자면, 앞서 PCA가 찾아내야 하는 A는 공분산 행렬을 통해 구합니다. 공분산 행렬은 데이터의 구조를 기술하는 수학적인 방법을 제공합니다. 공분산은 서로 다른 두 변수가 어떤 상관관계를 가지고 있는지를 알 수 있기 때문에, 데이터의 분포에서 중심이되는 축들을 구할 수 있도록 도와줍니다.
시그마 를 X의 공분산 행렬이라 정의하고 A행렬의 크기를 1이라고 제한하면, Z의 분산이 최대가 되는 A행렬을 찾기 위해 X의 공분산행렬과, A가 사용되는 것을 알 수 있습니다.

이 식이 a에 대해 최대가 되는 부분을 구하기 위해 라그랑주 승수법을 도입한 방정식을 세우면 아래와 같습니다. (제약조건은 a벡터의 크기가 1인 부분을 이용하면 됩니다.)

극대가 되는 점을 구하기 위해 L을 a에 대해 편미분하고 값이 0이 되는 a를 찾으면, 그때의 a가 Z의 분산을 최대화 하는 것을 알 수 있습니다. (일반적으로 공분산행렬은 Positive-Semidefinte 한 성질을 갖는 행렬인 것이 알려져 있습니다.)

따라서 위 식으로부터 a는 X의 공분산행렬의 고유벡터로 구성된다는 사실을 알 수 있습니다. 고유벡터와 고유값의 성질에 의해, 고유값이 클수록 해당 고유벡터가 나타내는 축이 데이터의 분산에 많은 영향을 끼친다는 것을 알 수 있습니다.
정리하면, 다음과 같습니다.
1. X를 차원축소한 Z의 분포를 최대화 하는 A를 찾는 것이 PCA의 목표.
2. A는 X의 공분산행렬의 고유벡터로 이루어짐.
3. 고유벡터에 해당하는 고유값이 클수록 고유벡터가 데이터의 분포를 잘 반영하는 것으로 해석할 수 있음.
Dimensionality Reduction
PCA를 통해 차원축소를 하려 할 때, 일반적으로 축소될 차원을 선택하는 기준은 전체 데이터의 분산의 90% 정도까지 반영하는 차원 k를 찾는 것으로 알려져 있습니다. 분산을 90%정도 보존하는 차원 축소는 데이터의 분포를 학습하기 적절한 정도로 유지하고 있다고 보고 축소된 데이터를 사용하는 것입니다.
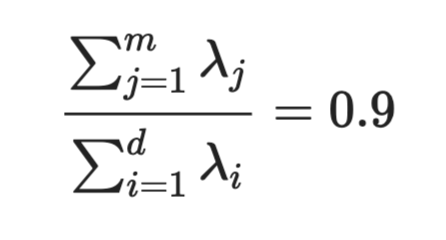
Conclusion
PCA는 차원축소의 방법을 제시함으로써, 데이터의 분산(분포)를 최대한 유지하면서 데이터의 크기를 줄이는 효율적인 방법을 제시하였습니다. 차원축소는 데이터 공분산행렬의 고유벡터들을 이용해서 이루어지며, 분산을 90% 정도 보존하는 선에서 축소할 차원이 결정됩니다.
'Artificial Intelligence' 카테고리의 다른 글
| [TITANIC] 타이타닉 생존자 예측 모델 (0) | 2020.04.14 |
|---|---|
| [MNIST] Random Forest를 이용한 간단한 모델 만들기 (0) | 2020.04.12 |
| KNN Algorithm with Data-Driven k Value (0) | 2020.04.01 |
| KNN (K-Nearest Neighbor) (0) | 2020.03.29 |
| Image Classification Pipeline (0) | 2020.03.28 |