2020. 4. 1. 21:29ㆍArtificial Intelligence
KNN Algotirhm with Data-Driven k Value (2014) Debo Cheng, Shichao Zhang. et al 을 리뷰한 포스팅임을 서두에 밝힙니다.
Abstract
KNN 알고리즘이란, 머신러닝이나 딥러닝 분야에서 주어진 Sample을 분류(Classification)할 때 사용하는 방법입니다. 기존에 가지고 있던 테스트 샘플들과의 거리를 측정(L1 norm, L2 norm등 거리를 측정하는 다양한 방법이 있음)하여, 거리가 가장 가까운 K개의 샘플을 선택하고 그 K개의 샘플중에서 가장 많은 샘플이 속한 클래스의 레이블을 주어진 Sample의 레이블로 결정하는 방법입니다. ( 더 자세한 내용은 KNN에 대한 포스팅을 참고해주세요 )
기존의 KNN알고리즘은 모든 테스트 케이스에 대해서 고정된 K값을 유지한다는 특징을 가지고 있습니다. 즉 Grid Search나, Random Search등의 방법으로 찾은 HyperParameter인 K가 모든 테스트 샘플에 대해서 동일하게 적용된다는 점입니다. 이러한 방식은 테스트 샘플과 트레이닝 샘플 사이의 상관관계(Corrrelation)을 무시하고, K를 고정해버림으로써 KNN을 이용한 Classification작업의 정확도를 낮추는 원인으로 작용하게 됩니다.
논문에서 제시하는 S-KNN(Sparce learning based KNN)은 테스트 샘플과 트레이닝 샘플 사이의 상관관계를 고려하여 테스트 샘플을 Recponstruct하고, 그 과정에서 각각의 테스트 샘플마다 가장 적합한 K값을 찾아서 분류하는 방식을 사용합니다. 다시말해서, 테스트 케이스마다 최적의 K값을 학습하여 분류한다는 의미입니다.
Introduction
앞서 Abstract에서 언급했듯, KNN알고리즘의 핵심 원리는 서로 가까이 있는 샘플들일 수록 같은 클래스로 분류될 가능성이 높다는 것입니다. 분류해야 하는 샘플과 K번째까지 가까운 이웃들을 골라서 그중에 다수표를 차지하는 클래스의 레이블로 분류하는 이 방식은, 명시적인 훈련 과정이 없는 알고리즘으로 잘 알려져 있습니다. 그저 테스트 샘플을 분류할때 저장된 기존의 데이터들과 거리를 계산해주기만 하면 되기 때문입니다. (자세히 : KNN 시간복잡도)
기존 KNN알고리즘의 단점은 K값이 어떻게 선택되느냐에 따라서 해당 클래스의 분류 결과가 상당히 달라질 수 있다는 점입니다. 즉, K값이 어떻게 선택되느냐에 따라서 정확도가 민감하게 영향을 받는다는 것입니다. 아래 그림에서 k값이 5로 주어지느냐, 3으로 주어지느냐에 따라서 ?로 표시된 샘플이 분류되는 결과값은 달라지게 됩니다.

적절한 K를 선택하는 알고리즘이 여러 논문들에 의해 발표된 바가 있으나, 어떤 경우에서든 들어맞는 알고리즘은 찾기가 어렵고, 이 또한 모든 테스트 샘플에 대해서 일괄적으로 적용할 경우에 만족할 만한 성능이 나오지는 않는 것으로 알려져 있습니다.
KNN은 K값에 따라서 결과가 바뀔 가능성이 큰 알고리즘이기 때문에, K값을 한번 결정하고 나서 그 값을 모든 테스트 케이스에 동일하게 적용하는 것은 KNN 의 정확도를 낮추는 원인이 됩니다. 따라서 논문의 저자는 K값을 테스트 샘플마다 다르게 설정하여 이를 개선하고자 하였습니다.
K값을 테스트 샘플마다 다르게 설정하기 위해서 저자가 주장하는 방법은 아래와 같습니다.
1. 트레이닝 데이터와 테스트 데이터의 상관관계(Correlation)를 고려한다.
2. 트레이닝 데이터의 Local Structure를 보존한다. (LPP를 사용)
3. 1번과 2번 과정을 반영해서 테스트 샘플을 Reconstruct한다.
4. Reconstruct된 테스트 샘플을 통해 적절한 K값을 찾아낼 수 있고, 이를 KNN알고리즘에 적용한다.
이 방법은 기존의 방법이 데이터의 분포 및 상관관계를 무시한 것과 다르게, 이를 보존하여 적절한 K를 찾는데 사용했다고 요약할 수 있습니다.
Method & Algorithm
$n = training, m = test d = dimension$ 이라고 정의하고 $X$를 $n * d$ 크기를 가지는 트레이닝 셋 행렬, $Y$를 $m * d$ 크기를 가지는 테스트 셋 행렬, $W$를 $n * m$ 크기를 가지는 트레이닝 셋 - 테스트 셋 Coefficient 행렬이라고 정의합니다.
$W$를 통해 트레이닝 셋을 테스트 셋이 가지는 차원으로 매핑(mapping)할 수 있습니다. 이때 $W$ transform의 목표는 트레이닝 셋과 테스트 셋의 상관관계를 고려하여 트레이닝 셋이 해당 테스트 셋과 비슷한 상관관계를 갖도록 변환하는 것입니다.
또한 동시에, 트레이닝 셋을 테스트 셋으로 변환하면서 트레이닝 셋들끼리의 상관관계를 최대한 보존하도록 변환합니다.
다시 말해서, 트레이닝 셋 내에서의 서로의 관계를 유지하면서 테스트 셋과 높은 상관관계를 보이도록 변환하는 $W$를 구하는 것입니다.
이렇게 해서 얻은 $W$를 통해 각각의 테스트 샘플에 대해 가장 적합한 K를 찾을 수 있습니다. ( $W$가 트레이닝 샘플과 테스트 샘플의 상관관계를 보여주므로, 이 값을 통해서 가장 깊게 연관되어 있는 K개를 선택할 수 있습니다. )
따라서 위 목적에 맞는 $W$를 구하는 것이 이 논문의 핵심 알고리즘임을 알 수 있습니다.
Objective Function (Eq.7)
최적화된 $W$를 찾기위한 목적함수(Objective Function)은 다음과 같습니다.

식의 각 항을 (1), (2), (3)으로 나누고 각각을 살펴보겠습니다.
1. Minimize difference between $Y$ and $W^tX$ (1), (3)
첫 번째 식은 트레이닝 셋과 테스트 셋의 상관관계를 잘 반영하기 위한 것입니다. (1)번식의 값이 작아질수록, $W$를 통해 트레이닝 셋을 테스트 셋의 공간에 매핑한 값이 테스트 셋과 유사하다는 것을 의미하므로, 서로 상관관계가 커지는 것을 의미하기 때문입니다.
$Y$의 값이 커짐에 따라 $W^tX$ 값이 같이 커진다는 것은 $W$가 테스트셋과 트레이닝 셋의 상관관계를 높게 만들었다는 것을 의미합니다. (3)번항목의 경우 1번 항목을 계산하다보면 나오게 되는 역행렬의 존재가 항상 100% 보장되지 는 않기 때문에 역행렬로 근사해 주기 위해서 넣어준 식입니다.
2. Locality Preserving Projection (LPP) (2)
두 번째 식은 트레이닝 셋의 Original Local Structure를 잘 보존하기 위한 식을 의미합니다.
해당 내용은 다른 논문에 Reference 된 것으로서 이번 포스팅에서는 자세히 다루지는 않겠습니다. 다만 이 두번째 식의 존재가 훈련 과정에서 트레이닝 셋의 원래 분포를 잘 반영하도록 함으로써, 기존의 트레이닝셋의 분포를 따르면서 테스트 샘플과 높은 상관관계를 갖도록 하는데 도움을 준다는 점이 중요합니다.

위 식을 통해 얻은 $W$에서 테스트 샘플마다 최적화된 K값을 구할 수 있으며 그 값을 이용하면 KNN알고리즘의 정확도를 높일 수 있다는 것이 이 논문에서 주장하는 핵심 알고리즘입니다.
Conclusion & Comment
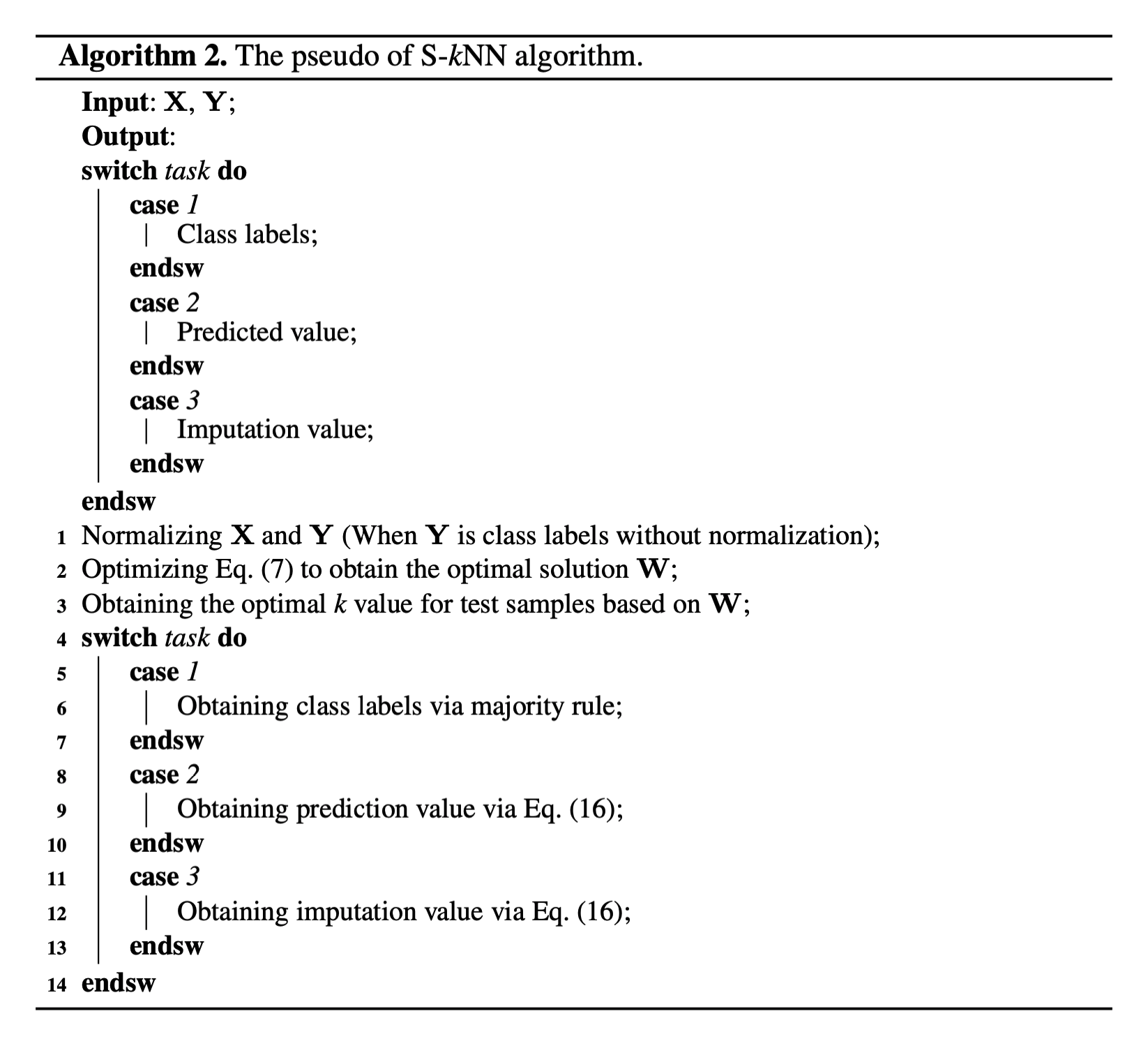
Classification, Regression, Missing data Imputation 이 3가지 항목에서 테스트해 본 결과, s-KNN 방식이 기존의 KNN방식보다 높은 성능을 나타내는 것을 확인할 수 있습니다.
테스트 셋과 트레이닝 셋의 상관관계를 고려해서, 트레이닝 셋의 분포를 최대한 유지하면서 둘 사이의 상관관계를 높게 유지하는 W를 구해 적절한 K를 테스트 샘플마다 다르게 고르는 방식은 기존의 K선택 방법보다 더 나은 결과를 제공합니다.
'Artificial Intelligence' 카테고리의 다른 글
| [MNIST] Random Forest를 이용한 간단한 모델 만들기 (0) | 2020.04.12 |
|---|---|
| Principal Component Analysis(PCA) (1) | 2020.04.02 |
| KNN (K-Nearest Neighbor) (0) | 2020.03.29 |
| Image Classification Pipeline (0) | 2020.03.28 |
| Markov Decision Process (MDP) (0) | 2020.03.28 |