2020. 3. 21. 12:49ㆍComputer Science/Problem Solving (PS)
풀이
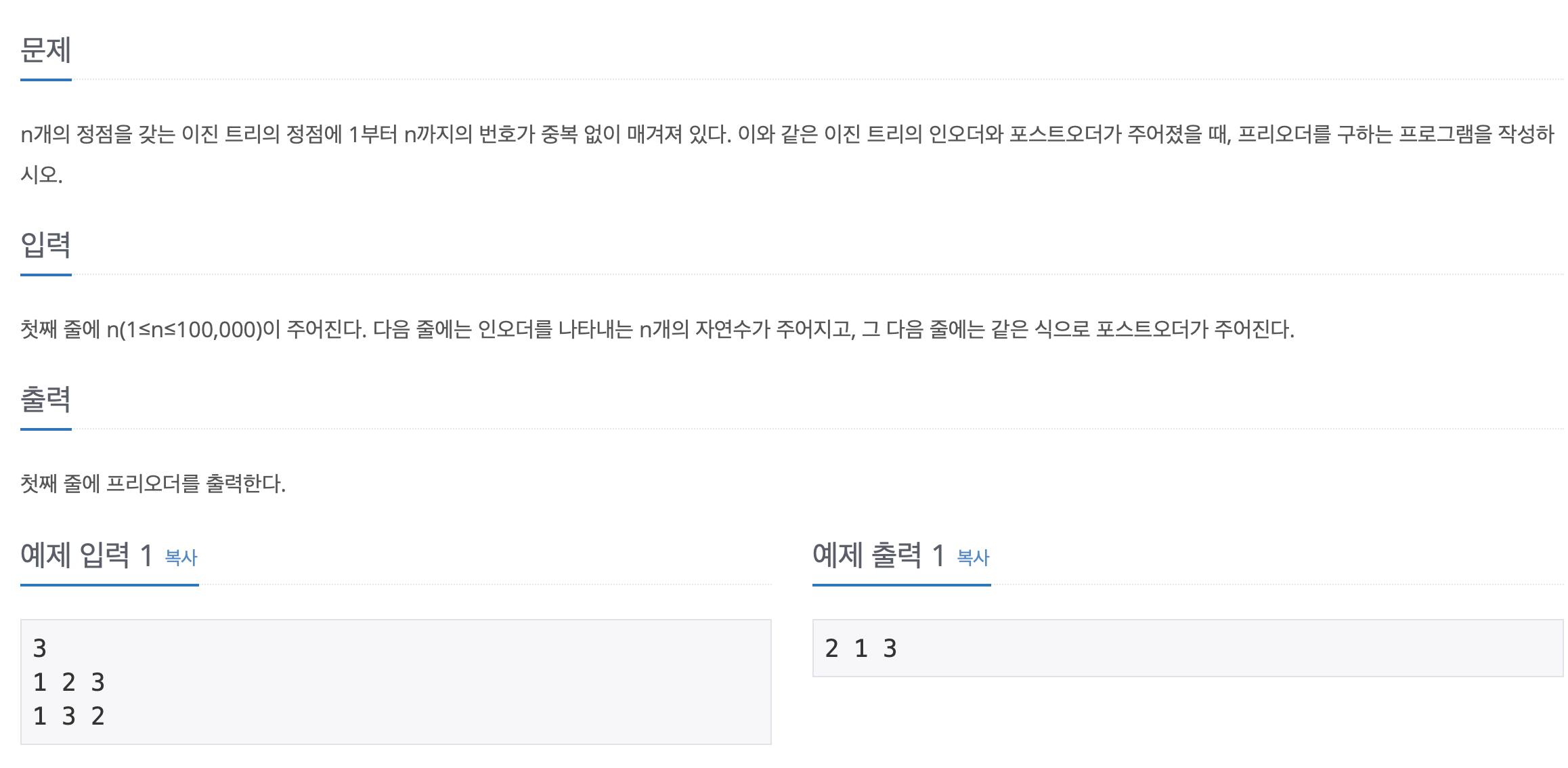
트리의 중위 순회(InOrder), 후위 순회(postOrder)의 성질을 이용하여 전위 순회(preOrder)의 결과를 출력하라는 문제입니다. 중위 순회와 후위 순회를 이용해서 직접 트리를 생성한 후에 그냥 전위 순회를 재귀적으로 호출하는 방법도 있겠지만, 이 방법은 트리를 생성해야 하기 때문에 귀찮고 비효율적인 작업이 될 가능성이 보여서 다른 방법으로 문제를 해결하였습니다.
트리의 중위 순회는 트리의 모든 데이터를 일차원 직선에 사영했을 때, 그 결과를 순차적으로 보여준다는 특징이 있습니다.
정렬된 이진 탐색 트리의 경우 트리의 중위 순회 결과는 숫자 배열을 정렬된 순서대로 출력합니다.
트리의 후위 순회는 재귀적인 방식으로 Left child -> rightChild -> Parent Node의 순서를 지켜가면서 탐색하기 떄문에 후위 순회 결과의 제일 마지막 인덱스에는 항상 Root Node의 값이 들어가게 됩니다,
위 문제는 중위 순회와, 후위 순회의 이러한 특성들을 사용하여 간단한 재귀 함수로 구현할 수 있습니다.
1. inOrder의 결과를 배열에 입력받습니다. 입력받으면서, 입력받는 데이터가 몇 번째 데이터인지에 대한 인덱스 정보를 findRoot배열에 같이 저장합니다.
> inOrder 배열을 입력받으면서 입력받는 숫자의 인덱스를 기록해 놓는 이유는 나중에 Parent Node를 재귀적으로 찾을 때, 이 인덱스를 이용하기 때문입니다.
2. postOrder의 결과를 배열에 입력받고 calc함수를 호출하도록 합니다.
3. calc함수는 파라미터로 들어온 인덱스를 통해 해당 서브트리(처음에는 전체트리)의 root를 찾고, 해당 서브트리의 왼쪽 서브트리의 root를 찾고, 오른쪽 서브트리의 root를 찾는 과정을 재귀적으로 반복합니다.
> 왼쪽 서브트리의 root를 찾는 이유는 preOrder의 특징 때문입니다. preOrder는 Root -> Left child -> Right Child의 순서대로 탐색을 진행합니다.
소스 코드 (C++)
#include <iostream>
using namespace std;
int postOrder[100001];
int inOrder[100001];
int findRoot[100001];
int n;
void calc(int start, int end, int start2, int end2) {
if (start > end) return;
int root = postOrder[end2];
cout << root << " ";
int pos = findRoot[root];
calc(start, pos - 1, start2, start2 + (pos - 1 - start));
calc(pos + 1, end, start2 + pos - start, end2 - 1);
return;
}
int main() {
cin >> n;
for(int i=0;i<n;i++){
cin >> inOrder[i];
findRoot[inOrder[i]] = i;
}
for(int i=0;i<n;i++) cin >> postOrder[i];
calc(0, n-1, 0, n-1);
return 0;
}'Computer Science > Problem Solving (PS)' 카테고리의 다른 글
| [백준 3653 | 펜윅 트리] 영화 수집 (0) | 2020.06.17 |
|---|---|
| [백준 2042] 구간 합 구하기 (0) | 2020.06.14 |
| [BOJ_10814 | Stable Sort] 나이순 정렬 (0) | 2019.07.10 |
| [BOJ_1182 | DFS backtracking] 부분집합의 합 (0) | 2019.02.15 |
| [BOJ_10799 | Stack] 쇠막대기 (0) | 2019.02.15 |