[BOJ_10814 | Stable Sort] 나이순 정렬
2019. 7. 10. 00:56ㆍComputer Science/Problem Solving (PS)
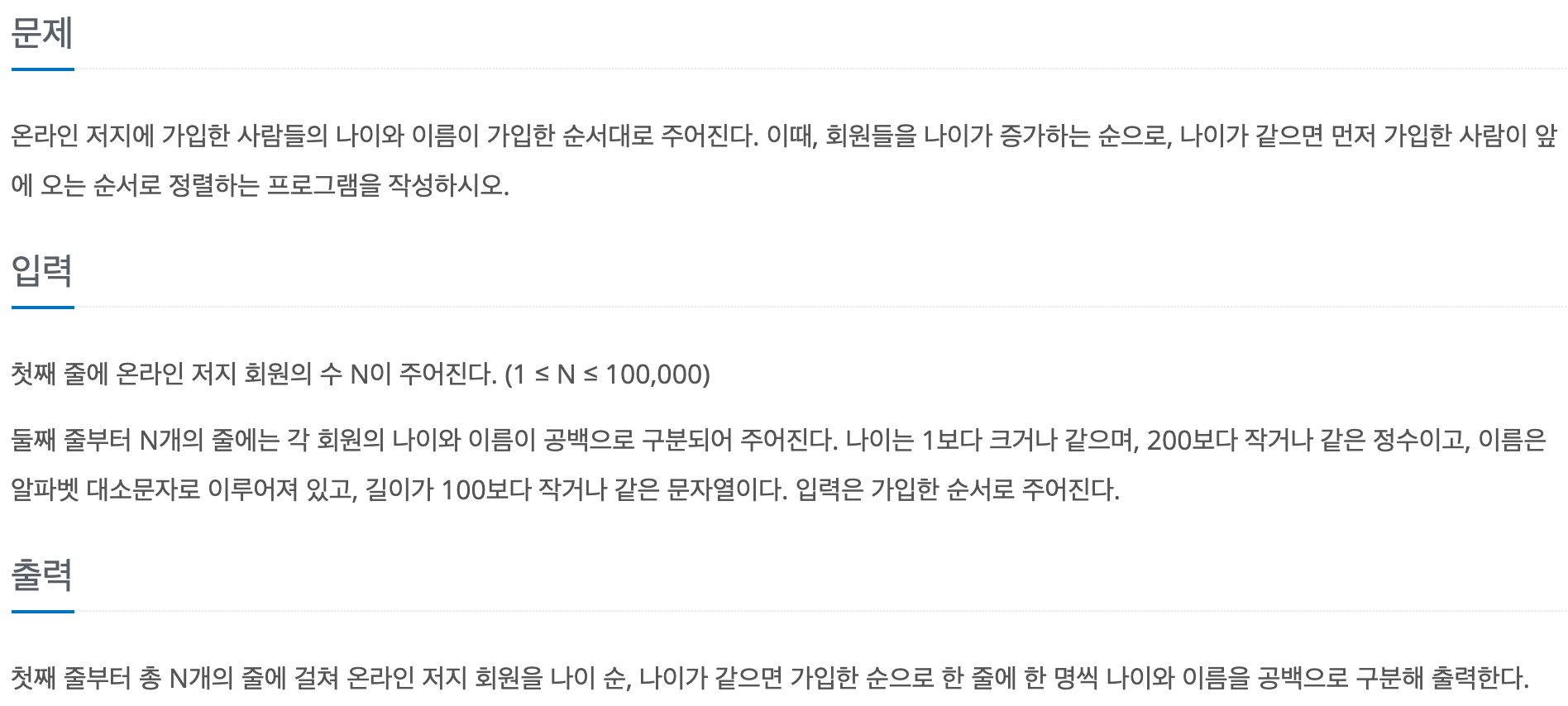
풀이
stable sort를 통해 구현한다면 쉽게 해결할 수 있는 문제이다.
Stable Sort란 정렬 알고리즘의 종류가 아닌 알고리즘의 정렬 방식에 관한 것으로
동일한 키 값을 가진 원소들에 대하여 정렬하기 전과 정렬하기 후의 value가
같은 순서를 가지도록 정렬하는 방식을 의미한다.
예를 들어 [key, value] 쌍을 갖는 객체들이 다음과 같이 나열되어 있다고 하자
[3, "철수"] [2, "영희"] [1, "훈이"] [2, "맹구"], [2,"뚱이]
key값에 대하여 위 객체들을 오름차순으로 정렬한다고 할 때, Stable Sort는 객체들을 다음과 같이 정렬한다.
[1, "훈이"] [2, "영희"] [2, "맹구"] [2, "뚱이"] [3, "철수"]
즉, key 값이 동일한 경우 정렬되기 전의 객체의 순서를 보존한다는 것이다.
Unstable Sort의 경우에는 동일한 키 값에 대하여 정렬되기 이전의 순서를 보장하지 않기 때문에
위 문제를 해결하기 위해서는 Stable Sort를 이용해야 한다.
Stable Sort의 예시로는 Bubble Sort, Merge Sort등이 있으며,
quick sort, heap sort 등은 Unstable Sort 에 속한다.
소스 코드
import java.util.*;
public class BOJ_10814 {
public static void main(String[] args){
Scanner input = new Scanner(System.in);
int n = input.nextInt();
User[] user = new User[n];
User[] temp = new User[n];
for(int i=0;i<n;i++){
int age = input.nextInt();
String name = input.next();
user[i] = new User(age, name);
}
mergeSort(user, temp, 0, n-1);
for(int i=0;i<n;i++){
System.out.println(user[i].age+" "+user[i].name);
}
}
public static void mergeSort(User[] arr, User[]temp, int left, int right){
if(left<right){
int mid = (left+right)/2;
mergeSort(arr, temp,left, mid);
mergeSort(arr, temp,mid+1, right);
merge(arr, temp,left, mid, right);
}
}
public static void merge(User[] arr, User[] temp, int left, int mid, int right){
int l = left; int m = mid+1; int k = left; int n = right+1;
while(l<=mid && m<=right){
if(arr[l].age<=arr[m].age) temp[k++] = arr[l++];
else temp[k++] = arr[m++];
}
while(l<=mid)
temp[k++] = arr[l++];
while(m<=right)
temp[k++] = arr[m++];
for(int i=left;i<right+1;i++){
arr[i] = temp[i];
}
}
}
class User implements Comparable<User>{
int age;
String name;
User(int age, String name){
this.age = age;
this.name = name;
}
@Override
public int compareTo(User o) {
if(this.age < o.age) return -1;
else if(this.age > o.age) return 1;
else return 0;
}
}
반응형
'Computer Science > Problem Solving (PS)' 카테고리의 다른 글
| [백준 2042] 구간 합 구하기 (0) | 2020.06.14 |
|---|---|
| [백준 2263] 트리의 순회 (0) | 2020.03.21 |
| [BOJ_1182 | DFS backtracking] 부분집합의 합 (0) | 2019.02.15 |
| [BOJ_10799 | Stack] 쇠막대기 (0) | 2019.02.15 |
| [BOJ_14889 | DFS & BackTracking] 스타트와 링크 (0) | 2019.02.14 |