2020. 6. 17. 22:33ㆍComputer Science/Problem Solving (PS)

풀이
펜윅 트리로 검색해서 들어갔던 문제이기 때문에 어떻게든 펜윅 트리를 사용해서 풀어야 한다는 강박관념이 있었던 문제였습니다. 펜윅트리는 저번 포스팅에서도 간략하게 설명했지만 구간합을 빠르게 구하기 위해 사용되는 알고리즘입니다. 따라서 문제의 핵심은 특정 영화의 앞에 놓여있는 영화의 개수를 어떻게 구간합으로 표현할 것인가?입니다.
1. 영화는 한번의 시행때마다 그 위치가 움직이므로 위치의 변동을 표현할 수 있어야 한다.
2. 펜윅 트리는 구간의 합을 빠르게 구할 수 있는 자료구조이므로, 구간의 합을 영화 앞에 쌓여 있는 영화의 개수로 치환할 수 있어야 한다.
3. 영화의 위치가 변했을 때, 트리를 업데이트하기가 용이해야 한다.
위 생각을 적용해볼 때, n+m의 크기를 갖는 펜윅 트리를 구성하고, 특정 위치에 영화가 있는 경우는 1, 없는 경우는 0으로 표시한다면, 특정 영화의 위치까지의 부분합을 이용해서 특정 영화 위에 있는 영화의 개수를 구할 수 있게 됩니다. 이해를 돕기 위해 예제를 한번 살펴보도록 하겠습니다
n = 5, m = 3
꺼내는 영화의 번호 : 3, 1, 1
이 예제가 있다고 할 때, 펜윅 트리를 구성해보도록 하겠습니다. 우선 m개만큼 영화를 나중에 앞으로 이동시킬 것이기 때문에, 제일 앞의 m개의 공간은 0으로 비워 둡니다.
| idx | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| val | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 |
1번 영화의 위치는 4번이고, 2번 영화의 위치는 5번이라는 의미입니다. 이 표를 펜윅 트리로 표현하게 되면 아래와 같습니다.

여기서 3번째 영화를 꺼낸다고 하면, 우선 3번째 영화의 위치는 6이므로 펜윅트리에서 6까지의 부분합을 구합니다. 여기서는 2+1 = 3이 됩니다. 하지만, 자기 자신은 제외해주어야 하므로, 1을 빼주어 2로 구해주면 되는 것입니다. 즉 fenwickTree.sum(6)-1 이 되는 것입니다.
그리고 나서 3번째 영화는 앞으로 이동해야 하므로 제일 위의 부분인 3번 위치로 이동하게 됩니다. (이렇게 순서대로 영화를 하나씩 뺄 때마다 2번, 1번 위치로 차례대로 이동하는 것입니다.) 즉, 3번 위치의 값이 1이 되고, 기존의 6번 위치의 값은 3번째 영화가 빠졌으므로 0이 됩니다.
| idx | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| val | 0 | 0 | 3 | 1 | 2 | 0 | 4 | 5 |
이제 이 값을 기반으로 트리도 갱신해 주어야 합니다. 3번 위치에 값이 추가되었으므로 펜윅트리에서 영향을 받는 모든 부분을 갱신해 주어야 하고, 6번 위치에서 값이 빠졌으므로 마찬가지로 영향을 받는 모든 부분을 갱신해 주어야 합니다.
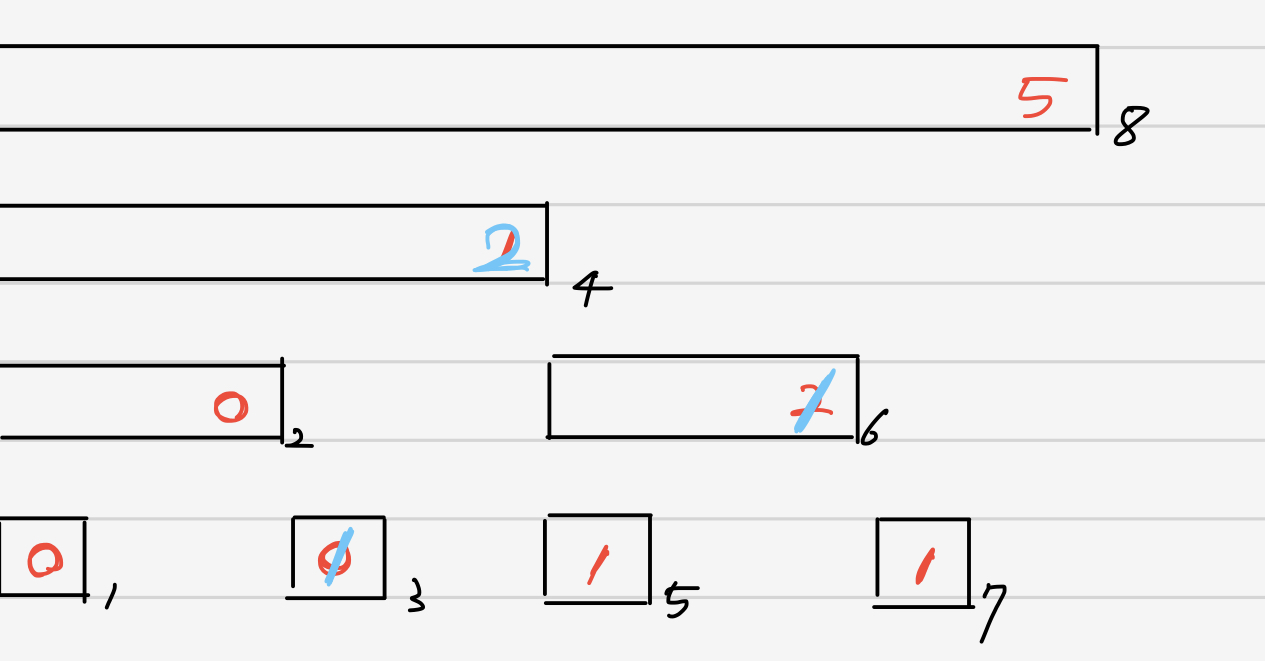
이 과정을 나머지 m번에 대해서 반복해 주면 문제를 해결할 수 있습니다.
소스코드 (JAVA)
import java.util.*;
public class BOJ_3653 {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int num = input.nextInt();
while(num > 0) {
num--;
int n = input.nextInt();
int m = input.nextInt();
int[] pos = new int[n+1];
FenwickTree fenwickTree = new FenwickTree(n+m+1);
// initialize pos arr & fenwick tree
for(int i=1; i<=n; i++){
pos[i] = i+m;
fenwickTree.add(i+m, 1);
}
for(int i=1; i<=m; i++){
int card = input.nextInt(); // the number of card
int posCard = pos[card]; // the actual location of card
System.out.print(fenwickTree.sum(posCard)-1 + " ");
pos[card] = m-i+1;
int afterPosCard = pos[card];
// feenwickTree update
fenwickTree.add(afterPosCard, 1);
fenwickTree.add(posCard, -1);
}
System.out.println();
}
}
}
class FenwickTree {
private int n, tree[];
FenwickTree(int n) {
this.n = n;
this.tree = new int[n+1];
}
public int sum(int pos) {
int result = 0;
while(pos > 0) {
result += tree[pos];
pos -= (pos & -pos);
}
return result;
}
public void add(int pos, int val) {
while(pos <= n) {
tree[pos] += val;
pos += (pos & -pos);
}
}
}
'Computer Science > Problem Solving (PS)' 카테고리의 다른 글
| [백준 13544 | 머지 소트 트리] 수열과 쿼리 3 (0) | 2020.06.21 |
|---|---|
| [백준 6549 | 세그먼트 트리] 히스토그램에서 가장 큰 직사각형 (0) | 2020.06.20 |
| [백준 2042] 구간 합 구하기 (0) | 2020.06.14 |
| [백준 2263] 트리의 순회 (0) | 2020.03.21 |
| [BOJ_10814 | Stable Sort] 나이순 정렬 (0) | 2019.07.10 |