2021. 10. 1. 22:02ㆍArtificial Intelligence
Full Stack Deep Learning의 2021 Spring Lecture를 정리합니다.

CNN
CNN(Convolutional Neural Network)은 합성곱(Convolution)을 사용하는 신경망의 한 종류로 "공간적" 정보를 유지한 상태로 정보를 다음 레이어로 보낼 수 있습니다. "공간적" 정보를 유지한 상태로 특징을 뽑아낼 수 있다는 장점 때문에 특히 이미지를 사용한 학습에 굉장히 유용합니다. 잘 알려진 이미지 분류 모델은 이렇게 Convolution Layer를 여러 겹 사용해서 모델의 특징들을 각각 뽑아내고, 뽑아낸 특징들을 바탕으로 FC(Fully Connected Layer)를 적용하여 이미지를 분류하는 형태를 띕니다.

Fully Connected Layer(FC)
일반적인 인공신경망 모델로 알려진 FC는 그 작동하는 방식으로 인해 이미지 분류(Image Classification)에서 가지고 있는 고질적인 문제가 있습니다. 바로 "공간적"정보를 인지하지 못하는 점입니다.
FC가 동작하는 방법은 아래와 같습니다.
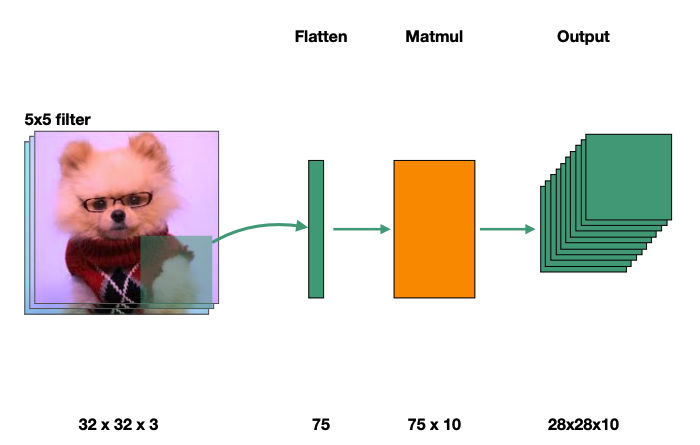
- 먼저 이미지를 width * height 크기의 1 Column Flatten Vector로 만듭니다. (아래 예제에서는 32 * 32 이미지를 1024 * 1 벡터로 만들었습니다.
- Vector의 길이 * Classify 해야하는 클래스의 개수를 크기로 하는 Feature 배열을 생성합니다. (아래 예제에서는 10개의 클래스가 있으므로 1024 * 10 크기의 배열이 학습시켜야 하는 Feature 파라미터의 배열이 됩니다.
- 반복된 학습을 통해 적절한 Feature 파라미터 배열을 만들고 나면 분류하고자 하는 이미지의 Flatten Vector를 Feature 파라미터 배열에 곱해서 Output Class를 통해 Classification을 수행합니다.

위의 과정에서 보았든 FC의 이미지 분류 과정은 2차원 이미지를 1차원 벡터로 변형한 다음 파라미터 연산을 수행함으로써 이미지를 이루는 픽셀과 픽셀 사이의 "공간적 정보"를 모두 제거한다는 특징이 있습니다. 아래 그림에 나오는 고양이를 우리가 눈으로 분류한다고 할 때는 눈을 이루는 픽셀의 2차원적 정보를 보고 저것이 고양이라고 인식하지만, 실제로 FC는 저 정보들을 일렬로 편 상태로 연산하기 때문에 공간적 정보를 활용할 수 없는 것입니다. 따라서 이미지를 상하좌우로 조금만 이동시켜도, 이를 일렬로 펴면 완전히 다른 값들을 가지기 때문에 FC는 해당 이미지를 완전히 다른 것으로 인식하는 경우도 많습니다.


또한 이미지의 크기가 조금만 커져도, 학습시켜야 하는 파라미터가 기하급수적으로 증가한다는 단점이 있습니다. 32*32 이미지를 학습시키기 위해서는 32 * 32 * 10(클래스 개수)개의 파라미터가 필요하지만, 1024*1024 이미지를 학습시키기 위해서는 1024*1024*10개의 파라미터가 필요합니다.
CNN은 수학의 "합성곱"연산을 사용해서 FC가 가지고 있는 단점을 해결하려합니다. (CNN의 등장이 곧 딥 러닝을 폭발적으로 성장시킨 계기이기도 합니다.)
What is Convolution
Convolution(합성곱) 이란, 원래 신호 처리에서 사용하는 방식으로 신호처리에서 사용하는 Convolution의 정의에 익숙하거나 Convolution을 처음 접하는 경우에 Convolution Layer에서 사용하는 방식이 조금 생소할 수 있습니다. 우선 Convolution에 정의에 대해 살펴보기 전에 알아야 할 것은 Convolution Layer에서 사용하는 Convolution 연산은 수학적 정의 그대로의 개념을 사용하는 것이 아닌 "의미상"의 개념, 즉 아이디어를 가져온 것이라는 점입니다. Convolution의 수학적 정의 그대로와 실제로 모델 레이어에서 사용하는 Convolution은 그 개념이 100% 동일하지는 않습니다.

위의 Convolution 연산의 도메인을 Time에서 Frequency Domain으로 이동시키면 Convolution Layer를 구성하는 의미로서의 Convolution을 조금 더 명확하게 이해할 수 있습니다. 도메인을 이동시키기 위해 널리 알려져 있는 라플라스 변환을 적용해보겠습니다. 라플라스 변환의 정의는 다음과 같으므로 함수 f, g에 각각 라플라스 변환을 적용해보면 Frequency Domain에서 f, g의 Convolution 연산이 Frequency Domain에서 두 함수의 스칼라 곱인 것을 확인할 수 있습니다.
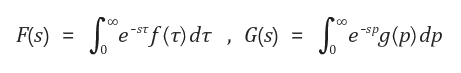





이를 이미지의 관점에서 생각해보면 다음과 같은 Insight를 얻을 수 있습니다.
- 이미지를 주파수 도메인으로 해석하면 x, y축으로 각각 뻗어나가는 픽셀의 밝기 변화를 기준으로 "파장"처럼 해석할 수 있게 된다.
- 주파수 도메인에서 F, G함수를 각각 이미지, 필터라고 해석해보면 두 함수의 곱은 "이미지의 특정 파장의 크기를 필터를 통해 조정하는 것" 정도로 해석할 수 있다.
즉 Convolution이라는 개념을 도입함으로써 특정 필터에 의해 조정된 이미지를 얻을 수 있는 것이고, 더 나아가 이 이미지의 결과를 통해 BackPropagation연산을 수행함으로써 필터도 학습시킬 수 있습니다.
How Convolution Layer Works
이미지와 필터 사이에 Convolution을 적용한 결과물인 Convolution Layer는 이미지 필터를 원본 이미지위로 미끄러지듯이 이동하면서 이미지 필터 배열과 해당 원본 이미지에 이미지 필터가 겹치는 부분의 배열을 곱하여 더하는 식으로 구할 수 있습니다. 자세한 계산 과정과 계산 과정의 수식은 널리 알려져 있으므로 아래 링크를 참조하시면 됩니다. (Stride, Padding, Pooling, Dilated Convolution은 이번 포스팅에서는 다루지 않겠습니다. 아래 링크에 자세한 설명이 나와있으니 참조해주세요)
(계산과정 예시)
CS231n Convolutional Neural Networks for Visual Recognition
Table of Contents: Convolutional Neural Networks (CNNs / ConvNets) Convolutional Neural Networks are very similar to ordinary Neural Networks from the previous chapter: they are made up of neurons that have learnable weights and biases. Each neuron receive
cs231n.github.io
5*5 이미지 필터를 32*32*3 (R, G, B) 이미지를 통과시키게 되면 (padding = 0, stride = 1) 28*28*1 의 아웃풋 레이어가 나오게 됩니다. 또한 서로 다른 필터(아래 그림의 주황색 부분)를 여러개 중첩시켜서 여러 레이어를 만든 이후에 이를 ReLu등의 비선형 함수를 통과시켜서 다음 Layer의 Input으로 사용하기도 합니다.

Benefits
필터를 적용할 때 x축, y축을 각각 이동하면서(Sliding) 연산을 수행하지만 연산을 보통 1*1, 2*2, 3*3, 5*5와 같은 2차원 배열의 단위로 수행하기 때문에 x축을 이동하더라도 인접한 y축의 이미지 픽셀도 연산에 포함되게 됩니다. 이를테면 위의 ConvolutionLayer Ouput인 28*28*1의 행렬의 (0,0,0)의 값의 계산 과정에는 원본 이미지의 (i, j, k)값이 모두 포함되게 되므로 "공간적 정보"를 저장할 수 있다는 것입니다. (i, j < 5 k<3)
또한 위에서 이야기 했듯, 해당 필터를 적용해 학습하는 과정에서 필터 자체가 학습 대상, 즉 BackPropagation이 적용되는 대상이기 때문에 학습을 할 수록 특정한 특징을 뽑아내는 필터의 성능도 좋아진다는 장점이 있습니다.
Standard Architectures
실제로 이미지 분류를 할때는 Convolution Layer, Activation Function, Pooling Layer, FullyConnected Layer등 여러 레이어를 차례로 통과시켜 분류를 하게 됩니다. Convolution Layer를 통과시켜 이미지에 특정 필터들을 적용한 결과물을 추출해내고, Activation 함수(일반적으로 ReLU)를 통과시켜 노드의 활성화 여부를 결정합니다. 그 이후에 Pooling을 통해 차원을 적절하게 축소하고, 마지막으로는 Fully Connected Layer를 통해 이를 Softmax 값으로 리턴하여 분류를 수행하게 됩니다.

Reference
'Artificial Intelligence' 카테고리의 다른 글
| Deep Residual Learning for Image Recognition (ResNet) - 2015 (0) | 2021.10.09 |
|---|---|
| ImageNet Classification with Deep Convolutional Neural Networks (AlexNet) - 2012 (0) | 2021.10.04 |
| [Ensemble] 앙상블 학습 (0) | 2020.04.27 |
| [RandomForest] 랜덤 포레스트란? (0) | 2020.04.27 |
| [RNN] Vanila RNN을 이용한 SPAM Filter구현 (0) | 2020.04.19 |