2021. 10. 9. 14:21ㆍArtificial Intelligence

Abstract
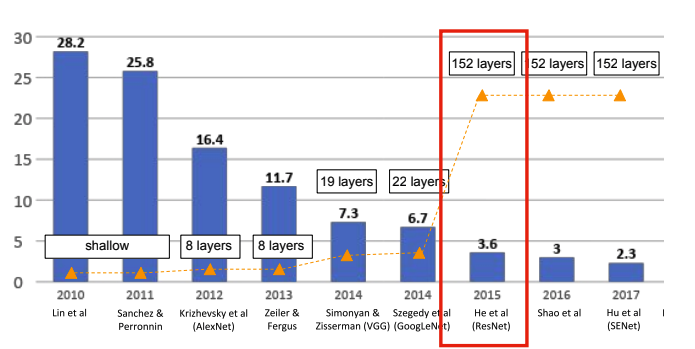
Neural Network(이하 NN)의 깊이가 깊어질수록 NN을 학습시키기가 어려워진다. NN의 깊이가 깊어질수록 조금 더 추상적인 Feature들을 학습시킬 수 있기 때문에 정확도가 향상될 것이라고 기대했지만, 아래의 그래프에서 볼 수 있듯, 깊이가 깊어질수록 나타나는 문제인 Vanishing / Exploading gradient등의 문제로 인해서 오히려 정확도가 낮아지는 모습을 보인다.

저자는 "Residual" Network는 최적화하기가 비교적 간단하며, 상당히 깊은 NN에서도 높은 정확도를 얻을 수 있다고 이야기한다. 실제로 ILSVRC 우승 모델들 중 ResNet을 사용한 모델부터 레이어의 개수가 22개에서 152개로 급격하게 증가한 것을 확인할 수 있다.
Introduction
여러 논문들 (위 논문이 Reference하고 있는)로 인해 Deeper한 모델일수록 성능이 좋다는 사실이 알려져 있다. (Deeper한 모델일수록 사물의 추상적인 Feature들을 잘 잡아낼 수 있다.) 하지만 위에서 소개했듯, 이러한 Deeper Layer에는 뚜렷한 단점이 존재하는데, 이것이 바로 vanishing / exploding gradients Problem이다. 이러한 문제는 normalized initialization, stochastic gradient descent 등의 방법들로 개선되어 왔고, 이번 논문에서는 이를 "Residual"(잔차)를 통해 해결하려고 한다.
Degradation Problem
네트워크가 깊어질수록 Accuracy(정확도)가 떨어지는 문제로 Train Error & Test Error가 둘다 낮다는 점에서 Overfitting과는 다른 문제이다. 이 문제를 해결하기 위해 저자는 "Deep Residual Learning Framework"라는 개념을 도입한다.
Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping.
기존의 레이어에서 Mapping하던 것을 H(x)라고 하면 Residual Network에서는 H(x) - x 를 Mapping하도록 제시한다. 즉 H(x) = F(x) + x의 형태인데, 이를 Residual Mapping(잔차 매핑)이라고 하며 이 Residual Mapping이 이존의 Mapping(H(x))보다 Optimize하기 쉽다는 것을 가정한다.
To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
Residual Learning에 대한 관점을 소개하는 맥락으로, 만약 identity mapping이 최적의 매핑이라면, non-linearg한 레이어를 여러개 쌓아서 identity mapping에 근접하게 training하는 것보다, F(x) + x의 형식으로 매핑하고 F(x), 즉 Residual을 0으로 근사하도록 하는 것이 개념적으로도 간단하다는 것을 의미한다. 이후에도 설명이 나오지만, zero-mapping보다 identity-mapping이 보다 더 optimal function에 가까울 것이라는 것이 전제되어 있다.
즉, Residual Block은 H(x)를 identity mapping에 근사하도록 하여 F(x)를 Residual function으로 보고 0으로 근사하도록 함으로써, 이전에 학습된 레이어의 정보를 그대로 가져온 상태로 남아있는 잔여 정보인 F(x)를 학습시키는 개념인 것이다.

Related Work
Residual, Shortcut Connection이 유용하게 사용된 사례들에 대해서 소개한다.
Residual Representations
For vector quantization, encoding residual vectors is shown to be more effective than encoding original vectors
It has been shown [3, 45, 46] that these solvers converge much faster than standard solvers that are unaware of the residual nature of the solutions.
Shortcut Connections
Practices and theories that lead to shortcut connections [2, 34, 49] have been studied for a long time. An early practice of training multi-layer perceptrons (MLPs) is to add a linear layer connected from the network input to the output [34, 49]. In [44, 24], a few intermediate layers are directly connected to auxiliary classifiers for addressing vanishing/exploding gradients.
Deep Residual Learning
Residual Learning
저자는 stacked layer가 H(x)에 근사하도록 하는 것보다, 이 레이어들이 residual function에 근사하도록 하는 것이 더 학습이 쉽다고 이야기한다. 실제로 Identity Mapping이 Optimal Function일 경우는 드물지만, 이 optimal function이 zero-mapping보다는 identity-mapping에 가깝다면, 다음과 같이 여러 개의 layer를 학습시켜 identity-mapping에 가깝게 만드는 것보다는 identity mapping을 optimal function으로 생각하고 F(x)를 잔차로 생각하여 이를 0으로 최적화하는 것이 의미상으로도, 계산상으로도 간단할 것이라는 것이다.
So rather than expect stacked layers to approximate H(x), we explicitly let these layers approximate a residual function F(x) := H(x) − x. The original function thus becomes F(x)+x. Although both forms should be able to asymptotically approximate the desired functions (as hypothesized), the ease of learning might be different.
Network Architectures
2개의 레이어를 하나의 Residual Block으로 간주하여 총 16개의 Residual Block을 사용하였다.

Reference
- [Paper]
'Artificial Intelligence' 카테고리의 다른 글
| 22-W12 Research Seminar (0) | 2022.03.22 |
|---|---|
| Going deeper with convolutions (GoogLeNet) - 2014 (0) | 2021.10.11 |
| ImageNet Classification with Deep Convolutional Neural Networks (AlexNet) - 2012 (0) | 2021.10.04 |
| [FSDL] CNNs (0) | 2021.10.01 |
| [Ensemble] 앙상블 학습 (0) | 2020.04.27 |