2020. 3. 24. 00:42ㆍArtificial Intelligence
Definition
마르코프 체인(Markov Chain)은 마르코프 성질(Markov Property)을 지닌 확률 과정을 의미합니다.
여기서 두가지 정의하 등장하게 됩니다. '마르코프 성질(Markov Property)', '이산 확률 과정(Discrete-time Stochastic Process).
마르코프 성질이라는 것은 현재의 상태가 오로지 바로 이전의 상태에만 영향을 받는 것을 의미합니다. 다시 말해, 이전의 상태가 바로 지금 현재의 상황을 결정하는 것이라고도 할 수 있는 것입니다.
확률 과정이라는 것은 '확률 분포를 가진 임의의 변수가 일정 시간 간격으로 값을 발생시키는 것'을 수학적으로 모델링하는 데에 사용되는 개념입니다. 예를 들어 주사위를 여러번 던지는 시행이 있다고 할 때, 주사위를 던져서 나오는 수는 확률 분포를 가집니다. 주사위를 연속적으로 던지면 "15242351..."등의 값을 발생시키게 되고, 이는 어떤 확률 분포를 통해 모델링된 값이라고 부를 수 있는 것입니다.
따라서 '마르코프 성질'을 가진 '확률 과정' 이라는 것은 현재의 값이 이전 값에 의해서 결정되는 모델에 의해 일정 시간 간격(timestep)마다 값이 생성되는 것을 의미하며, 이러한 성질 때문에 마르코프 체인은 마르코프 과정(Markov Process)라고도 불리게 됩니다.
(Reinforcement Learning에서는 Markov Process라는 말을 더 자주 사용합니다. 뒤에나올 MDP와도 깊게 연관됩니다.)
한 가지 주의할 사항은 '현재의 상태가 바로 이전의 상태에 의해 결정된다' 라는 말을 오해하면 안된다는 점입니다.
위 내용을 글자 그대로 해석하면 현재 상태가 A일때, 다음 상태는 A에 의해서 유일하게 결정되는, 다른 경우가 있을 수 없는 것이라고 오해할 수 있습니다. 그러나 핵심은 '유일하게 결정된다'가 아니라 '현재의 상태는 바로 직전의 상태에만 의존한다' 라는 점입니다.
다시 말해서, 이전에 아무리 많은 상태들이 있었어도 다음 상태에 영향을 미치는 것은 지금 현재 상태 뿐이라는 것을 암시하며, 지금 현재 상태에서 다음 상태를 결정할 때는 여러 가지 확률 변수들이 개입되게 되는 것입니다.
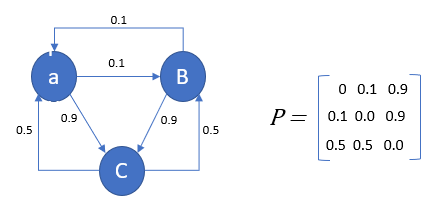
예를 들면, 위 그림에서 현재 상태가 'a'라고 할 때, 다음 상태를 결정하는 것은 a 이전의 어떤 상태가 아니라 오직 'a'이며, 'a'에서 특정한 확률을 거쳐 'B'가 될 수도 있고, 'C'가 될 수도 있는 것입니다.
따라서 이 마르코프 과정에서는 그림 오른쪽에 있는 상태전이확률행렬(state transition probability matrix)이 핵심이 됩니다.
Property
마르코프 체인은 정의에 의해 오직 2가지 속성으로 표현됩니다.
$X$ : 유한한 상태공간 집합
$P$ : 상태 전이 확률(state transition probability) : 모든 상태 사이의 전이 확률을 이용.
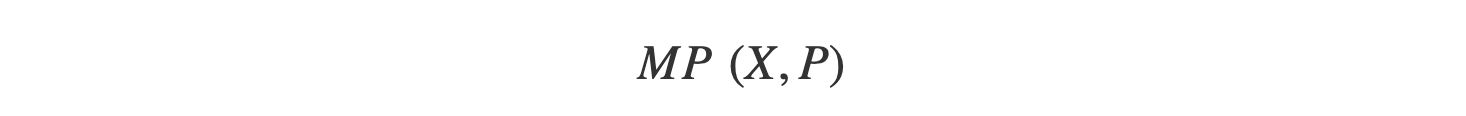
마르코프 성질은 다음과 같이 표현됩니다.
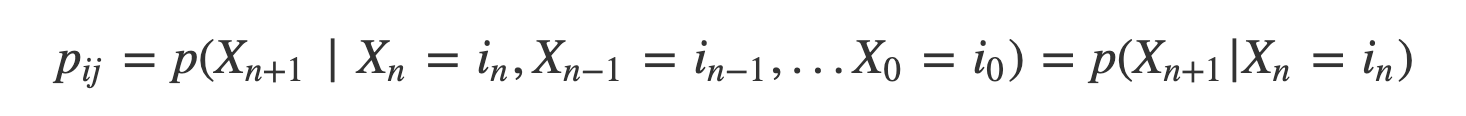
앞서 설명한 바와 같이 이전의 상태들은 다음의 상태를 결정하는데에 영향을 주지 못하는 것을 수식을 통해 확인할 수 있습니다.
마르코프 체인 자체는 수동적인 모델이기 떄문에, 즉 이전 상태에 의해 다음 상태가 결정되는 모델이기 때문에 사용자가 개입하여 모델에 변수를 제공할 여지가 거의 없어서 RL에서는 직접적으로 사용되고 있지는 않지만, Markov Property에 Reward를 도입한 MRP등의 모델의 근간이 된다는 점에서 RL로의 확장성을 보여주는 모델이라고 할 수 있습니다.
'Artificial Intelligence' 카테고리의 다른 글
| Image Classification Pipeline (0) | 2020.03.28 |
|---|---|
| Markov Decision Process (MDP) (0) | 2020.03.28 |
| Reinforcement Learning (0) | 2020.03.23 |
| Probability For Deep Learning (0) | 2020.03.21 |
| Generative Adversarial Network(GAN) (0) | 2020.03.20 |