[백준 2188 | 포드-풀커슨] 축사 배정
2020. 7. 8. 00:09ㆍComputer Science/Problem Solving (PS)
풀이
소와 축사와의 관계를 네트워크 그래프로 정의하는 것이 핵심이 되는 문제였습니다. 가장 많은 축사가 채워지는 것을 Source와 Dest간의 최대 유량을 결정하는 문제로 바꾸어주면 포드-풀커슨 알고리즘을 통해 이 문제를 쉽게 해결할 수 있습니다.
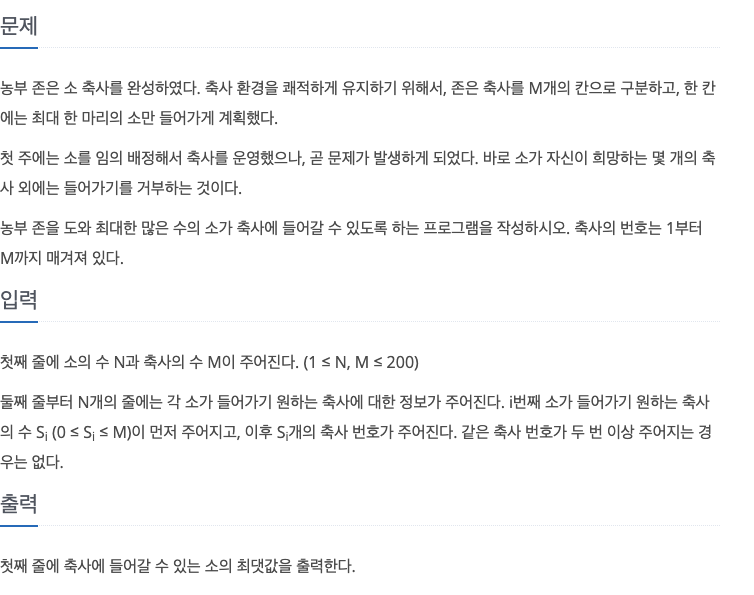
아래 그림과 같이 Source에서 모든 Cow로 가는 간선이 있다고 하겠습니다. (아래 그림에서의 모든 간선의 가중치는 1이 됩니다.)
Cow는 선호하는 Cage로 간선을 그릴 수 있으며 Source로부터 들어오는 Cow의 유량은 1이 되므로 여러 Cage로 가는 간선이 있다고 해도 결국에는 하나의 Cage밖에 선택할 수 없게 됩니다.
모든 Cage는 각각 Dest로 가는 가중치 1짜리 간선이 있습니다.
이 그래프에 따르면 가장 많은 우리가 채워지는 경우 = Source로부터 최대의 유량이 Dest로 흘러들어가는 경우가 되어
포드 풀커슨 알고리즘을 적용할 수 있습니다.

소스 코드(JAVA)
import java.util.*;
import java.io.*;
/*
@sckimynwa
*/
public class BOJ_2188 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer token = new StringTokenizer(br.readLine());
int n = Integer.parseInt(token.nextToken());
int m = Integer.parseInt(token.nextToken());
int size = n+m+2, source = 0, sink = n+m+1;
int[][] capacity = new int[size][size];
int[][] flow = new int[size][size];
// initial capacity
for(int i=1;i<=n;i++) capacity[0][i] = 1; // source to cow
for(int i=n+1;i<=n+m;i++) capacity[i][sink] = 1; // cage to sink
// cow to cage
for(int i=1;i<=n;i++){
token = new StringTokenizer(br.readLine());
int cage = Integer.parseInt(token.nextToken());
for(int j=0;j<cage;j++){
int cageIdx = Integer.parseInt(token.nextToken()) + n;
capacity[i][cageIdx] = 1;
}
}
int totalFlow = 0;
while(true) {
int[] parent = new int[size];
Queue<Integer> queue = new PriorityQueue();
for(int i=0;i<size;i++) parent[i] = -1;
parent[source] = source;
queue.add(source);
while(!queue.isEmpty() && parent[sink] == -1) {
int here = queue.poll();
for(int there = 0; there<size;there++) {
if (capacity[here][there] - flow[here][there] > 0
&& parent[there] == -1) {
queue.add(there);
parent[there] = here;
}
}
}
if(parent[sink] == -1) break;
int amount = Integer.MAX_VALUE;
for(int i = sink; i!=source; i=parent[i]) {
amount = Math.min(capacity[parent[i]][i] - flow[parent[i]][i], amount);
}
for(int i = sink; i!=source; i=parent[i]) {
flow[parent[i]][i] += amount;
flow[i][parent[i]] -= amount;
}
totalFlow += amount;
}
bw.write(totalFlow+"\n");
bw.close();
}
}
반응형
'Computer Science > Problem Solving (PS)' 카테고리의 다른 글
| [백준 6086 | 포드 풀커슨] 최대 유량 (0) | 2020.07.07 |
|---|---|
| [백준 1647 | MST] 도시 분할 계획 (0) | 2020.06.27 |
| [백준 1197 | MST] 최소 스패닝 트리 (0) | 2020.06.27 |
| [백준 13544 | 머지 소트 트리] 수열과 쿼리 3 (0) | 2020.06.21 |
| [백준 6549 | 세그먼트 트리] 히스토그램에서 가장 큰 직사각형 (0) | 2020.06.20 |