2020. 6. 21. 15:59ㆍComputer Science/Algorithm
Overview & Definition
머지 소트 트리는 백준 알고리즘 문제 13544 수열과 쿼리3 문제를 해결하기 위해서 사용하였던 자료구조입니다. 세그먼트 트리를 변형하여 만든 구조이기 때문에 초기화 하는 방법과, 쿼리 날리는 방법 등이 세그먼트 트리와 상당히 유사합니다.
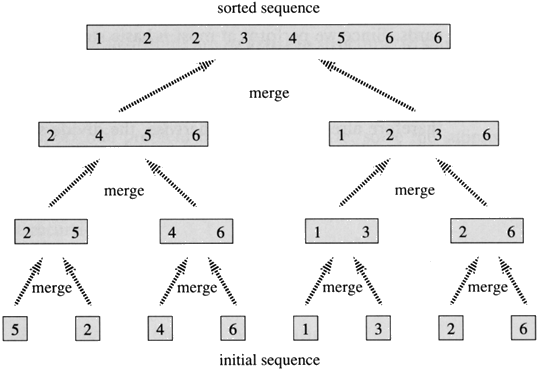
세그먼트 트리는 리프 노드(Leaf Node)에 각 배열의 원소를 집어넣고, 부모노드에 자식 노드들의 최댓값이나 최솟값, 혹은 부분합을 저장해서 특정 구간에 대한 질의(Query)를 빠르게 처리하는데 특화된 자료구조입니다. 머지 소트 트리는 부모 노드에 각 자식 노드를 머지한 결과값을 저장한 배열을 저장합니다. 예를 들어서 왼쪽 자식 노드가 [1, 3, 5], 오른쪽 자식 노드가 [2, 4, 6]인 상태라면, 부모 노드는 [1, 2, 3, 4, 5, 6]을 저장하게 되는 것입니다.
일반적인 세그먼트 트리가 하나의 노드에 하나의 값만 저장하는 것과는 다르게 하나의 노드에 배열을 저장한다는 것이 특징입니다. 또한 머지 소트가 이루어지는 중간 단계들을 저장하는 것이기 때문에 각 노드에 저장된 배열들은 모두 정렬되어 있음이 보장됩니다.
머지소트 트리의 초기화 코드는 다음과 같습니다.
초기화는 기존의 세그먼트 트리와 유사하게 재귀를 이용해서 작성합니다. 리프 노드일 경우에는 배열의 값을 그대로 넣어주고, 부모 노드일 경우에는 자식노드 둘의 배열을 머지한 결과를 넣어주면 됩니다.
public ArrayList<Integer> init(int left, int right, int pos) {
// in the case of the leaf node
if (left == right) {
tree[pos] = new ArrayList<>();
tree[pos].add(arr[left]);
return tree[pos];
}
int mid = (left + right) / 2;
ArrayList<Integer> leftArr = init(left, mid, pos * 2);
ArrayList<Integer> rightArr = init(mid+1, right, pos * 2 + 1);
return tree[pos] = merge(leftArr, rightArr);
}
두 배열을 머지하는 메서드 입니다. 머지 소트의 Merge함수와 거의 동일하게 구현된 것을 확인할 수 있습니다.
public ArrayList<Integer> merge(ArrayList<Integer> leftArr, ArrayList<Integer> rightArr) {
ArrayList<Integer> returnArr = new ArrayList<>();
int i=0, j=0, leftLen = leftArr.size(), rightLen = rightArr.size();
while(i < leftLen && j < rightLen) {
if (leftArr.get(i) <= rightArr.get(j)) {
returnArr.add(leftArr.get(i));
i++;
} else {
returnArr.add(rightArr.get(j));
j++;
}
}
while(i < leftLen) {
returnArr.add(leftArr.get(i));
i++;
}
while(j < rightLen) {
returnArr.add(rightArr.get(j));
j++;
}
return returnArr;
}Time Complexity
머지 소트 트리의 초기화 시간 복잡도는 머지 소트와 동일한 과정을 거치기 때문에 O(nlogn)을 가집니다. 그리고 쿼리를 날릴 경우에는, 어떠한 구간에 대한 쿼리를 요청하더라도 그 구간은 O(logn)개의 구간들의 조합으로 나눌수 있으므로 쿼리 요청에 대해서는 O((logn)^2)만큼의 시간이 걸리게 됩니다.
머지 소트 트리는 머지 소트의 모든 중간 단계를 저장하는 자료구조이기 때문에 O(nlogn)의 공간 복잡도를 갖습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| 최소 신장 트리 (MST) (0) | 2020.06.27 |
|---|---|
| 세그먼트 트리(Segment Tree) (0) | 2020.06.18 |
| 펜윅 트리(Fenwick Tree) (0) | 2020.06.14 |
| KMP 알고리즘 (0) | 2020.03.17 |